SIMERGE (Statistical Inference for the Management of Extreme Risks and Global Epidemiology) is a LIRIMA project-team started in January 2015.
It includes researchers from Mistis (Inria Grenoble – Rhône-Alpes, France), LERSTAD (Laboratoire d’Etudes et de Recherches en Statistiques et Développement, Université Gaston Berger, Sénégal), IRD (Institut de Recherche pour le Développement, Unité de Recherche sur les Maladies Infectieuses et Tropicales Emergentes, Dakar, Sénégal) and LEM lab (Lille Economie et Management, Université Lille 1, 2, 3, Modal, Inria Lille Nord-Europe, France).
Two scientific objectives
1. Spatial extremes, application to management of extreme risks
Weather variability, both in terms of space and time, is of prime importance hydrological, agricultural and energy contexts. Therefore, spatio-temporal modelling of environmental data is well studied in the literature. The basic objectives are: (i) to infer the nature of spatial variation of extreme precipitations and temperatures based on meteorological observations and (ii) to model the pattern of variability of these data components.
Different characterizations of multivariate extreme dependence structures have been proposed and these works were the basis of recent studies to characterize the dependence between extremes of a spatial process. Once the modeling step is achieved, the inference of the associated risk can be tackled. One of the most popular risk measures is the Value-at-Risk (VaR) introduced in the 90’s. In statistical terms, the VaR at level alpha corresponds to the upper alpha-quantile of the loss distribution.
Even though the VaR has been introduced to deal with financial risks, it is also of interest in meteorological applications where it is interpreted as a return level.
The Value-at-Risk however suffers from two main weaknesses. First, it provides us only with a pointwise information: VaR(alpha) does not take into consideration what the loss will be beyond this quantile. Second, random loss variables with light-tailed distributions or heavy-tailed distributions may have the same Value-at-Risk.
Consequently, the definition of new risk measures, the study of their properties in case of extreme events, i.e. when alpha tends to zero, and their estimation from data are three major statistical challenges.
2. Classification, application to global epidemiology
Only 23 of world’s countries have high-quality death registration data, and 75 have no cause-specific mortality data at all. Verbal autopsy is a thus a key technique for estimating the cause-of-death distribution in populations without medical death certification.
Symptoms along with causes of death are collected from a medical facility, and the cause-of-death D distribution is estimated in the population where only symptom data S are available. Since both D and S are usually qualitative measures, the estimation of the probability distribution of D given S can be seen as a classification problem for qualitative variables. In most cases, the number s of symptoms is high, S is a binary random vector of size s=100, leading to 2^s possible combinations of symptoms. The probabilistic modeling of S by, for instance, a multinomial distribution thus faces the curse of dimensionality: Moderate sample sizes do not allow an accurate estimation of all the 2^s probabilities. The challenge is then to build new probabilistic models sufficiently complex to handle complex dependences and yet sufficiently simple to be estimated in high dimension.
Principal Investigators
Stéphane Girard: Senior researcher, Mistis, Inria Grenoble Rhône-Alpes, France
Abdou Kâ Diongue: Professor, LERSTAD, UFR SAT Université Gaston Berger, Saint-Louis, Sénégal
Selected publications
[Objective 1] E. Deme, A. Guillou and S. Girard. Reduced-biased estimators of the Conditional Tail Expectation for heavy-tailed distributions. In M. Hallin
et al, editors, Mathematical Statistics and Limit Theorems, pages 105–123, Springer, 2015.
[Objective 2] S. Sylla, S. Girard, A. Diongue, A. Diallo and C. Sokhna. A supervised binary model-based classification method combining similarity measures
and mixture models, Dependence Modeling, 3, 240–255, 2016.
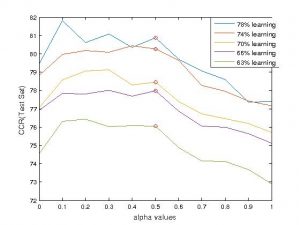
| Correct Classification Rate (CCR) obtained by the new classification method introduced in Sylla et. al (2016) on a verbal autopsy data set of 2,500 individuals characterized by s=100 binary variables and distributed in 22 classes. The method involves a nonlinear kernel which depends on a parameter alpha. For alpha=1/2, it reduces to the classical RBF kernel. As a comparison, a mixture model based on a multinomial distribution would lead to a CCR = 50%. |
Related events
- Financial and Actuarial mathematics conference in Mbour (Sénégal), july, 11th–15th, 2016: the conference was organized in collaboration with AIMS Senegal (African Institute for Mathematical Science) and the SWMA (Senegalese Women in Mathematics Association). Stéphane Girard and Aliou Diop where part of the scientific committee while Sophie Dabo Niang was part of the organizing committee. El Hadji Deme was an invited speaker. See https://sites.google.com/a/aims-senegal.org/workshop-swm-aims1/home
- CIMPA school « Méthodes statistiques pour l’évaluation des risques extrêmes: application à l’environnement, l’alimentation et l’assurance » in Saint-Louis (Sénégal), April, 5th–15th, 2016. The school was co-organized by Sophie Dabo-Niang and Aliou Diop. The scientific committee was headed by Stéphane Girard. See http://ecole-cimpa.univ-lille3.fr
PhD defences
[Objective 1] Pathé Ndao, « Modélisation de valeurs extrêmes conditionnelles en présence de censure », Université Gaston Berger, Sénégal, August, 2015.
[Objective 1] Aladji Bassene, « Contribution à la modélisation spatiale des événements extrêmes », Université Lille 3, May, 2016.
[Objective 2] Alessandro Chiancone, « Réduction de dimension via Sliced Inverse Regression: Idées et nouvelles propositions », Université Grenoble-Alpes, October, 2016.
[Objective 2] Seydou-Nourou Sylla, « Modélisation et classification de données binaires en grande dimension – Application à l’autopsie verbale », Université
Gaston-Berger, December, 2016.